Mean Median Mode Range Meaning | Measures of Central Tendency Understanding, Examples, and Formulas

Introduction Measures of Central Tendency, encompassing Mean Median Mode Range Meaning, stand as indispensable tools in statistical analysis, providing vital ...
Read more
Sample of Null Hypothesis|Examples and Explanations

1. Introduction to Sample of Null Hypothesis In the realm of statistical analysis and hypothesis testing, the concept of a ...
Read more
How to Find Correlation Coefficient in R | Mastering Correlation Analysis and Example
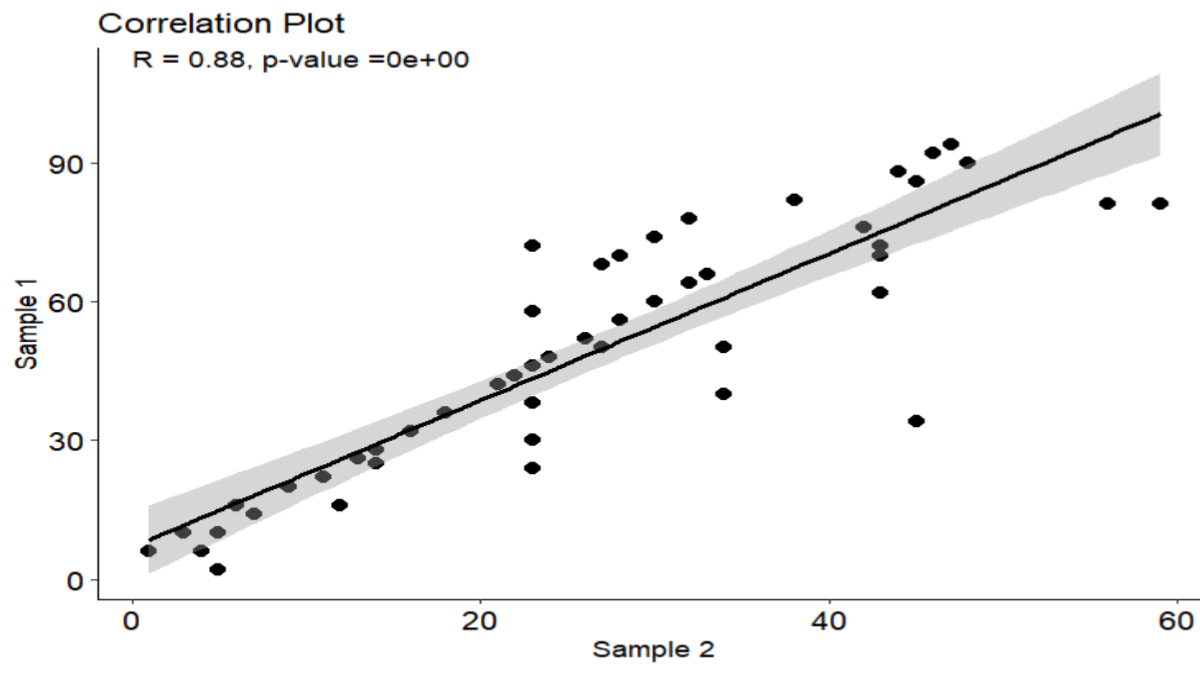
Introduction to Correlation Coefficient How to Find Correlation Coefficient in R is a common question among those involved in data ...
Read more
How to Find P Value from t Statistic: A Comprehensive Guide
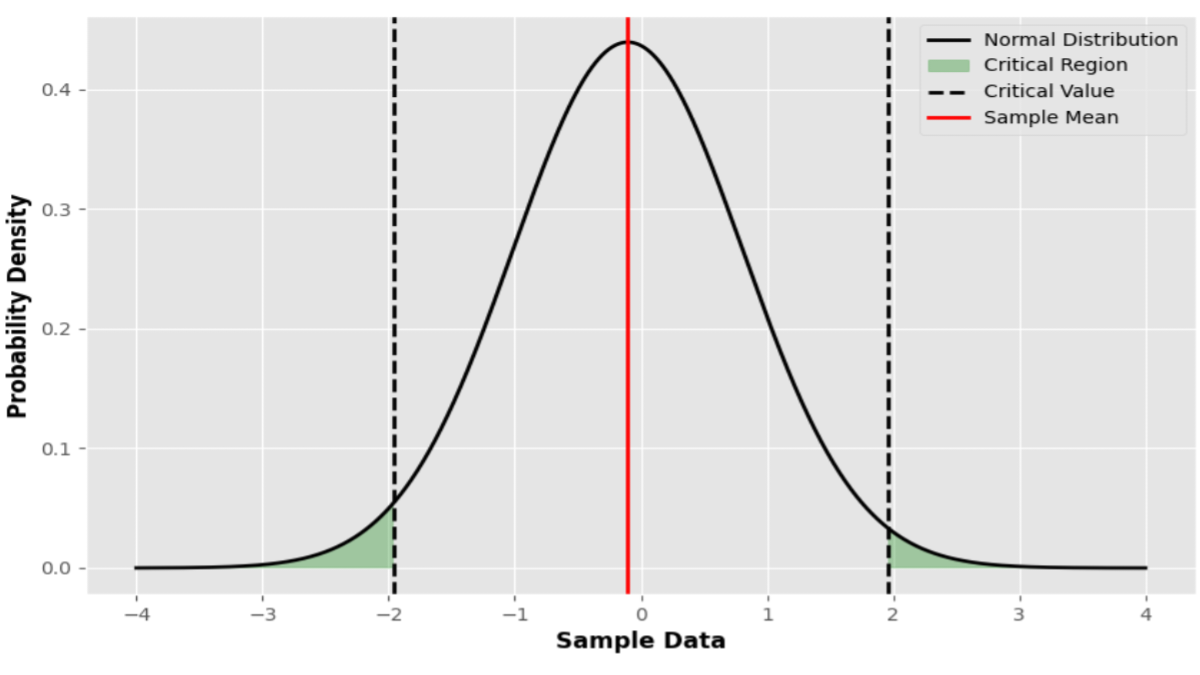
Introduction In the realm of statistics, the t-statistic and p-value are fundamental concepts that play a crucial role in hypothesis ...
Read more
Linear Regression in Machine Learning Python Code: A Comprehensive Guide for Mastery
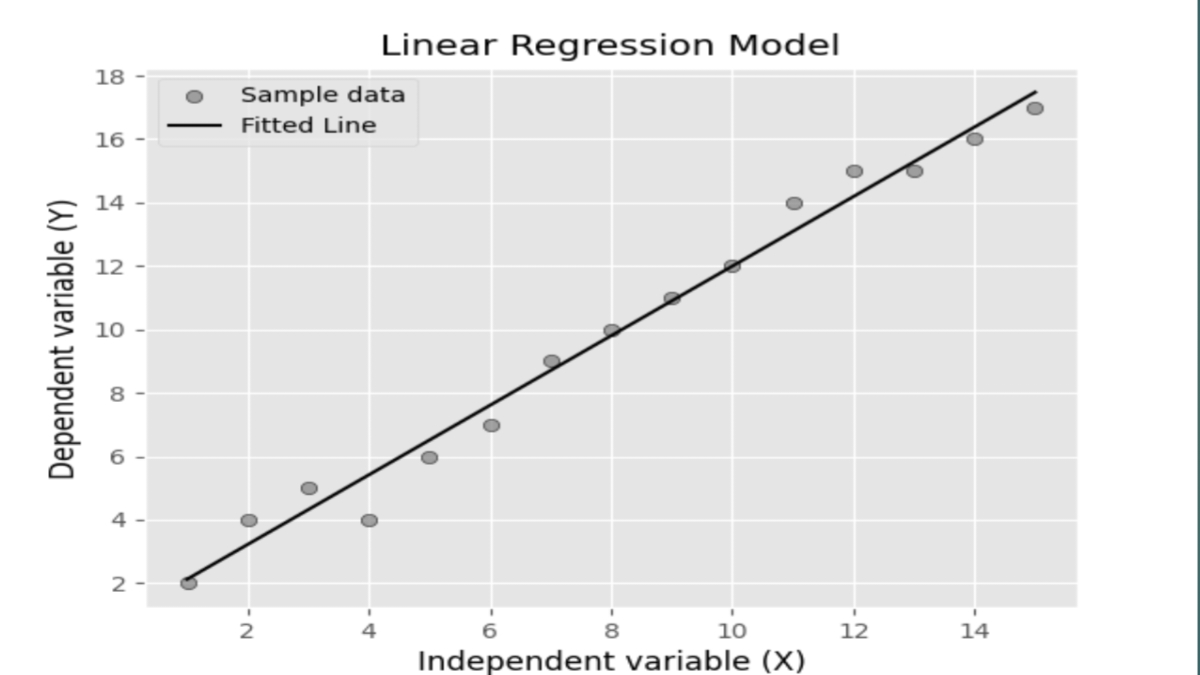
Introduction to Linear Regression Linear regression in machine learning Python, a cornerstone concept in the fields of machine learning and ...
Read more
Z Critical Value for 95 Confidence Interval | Understanding its Significance in Statistical Analysis
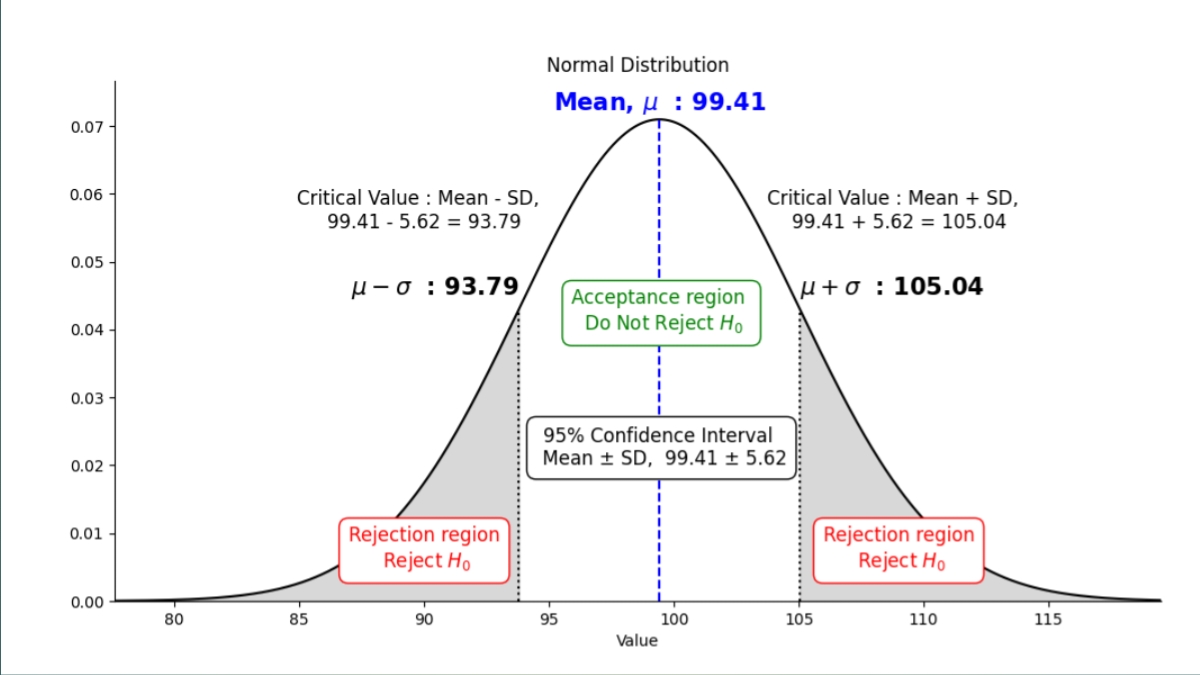
z critical value for 95 confidence interval
Read more
ARIMA Forecasting Model | Unlocking Future Trends with Time Series Analysis and Best Example Python Code
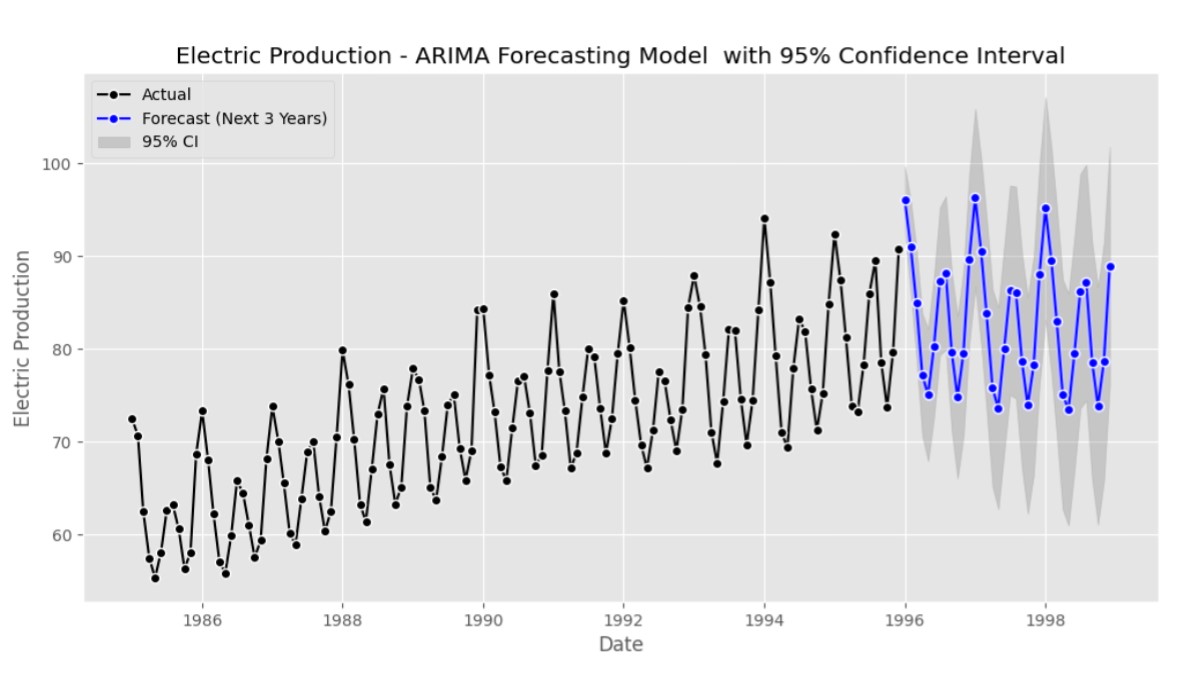
Introduction : In the ever-changing landscape of data analytics, the ARIMA (AutoRegressive Integrated Moving Average) forecasting model emerges as a ...
Read more
The Power of Data Analysis: Unveiling Positive Insights through Simple Example1
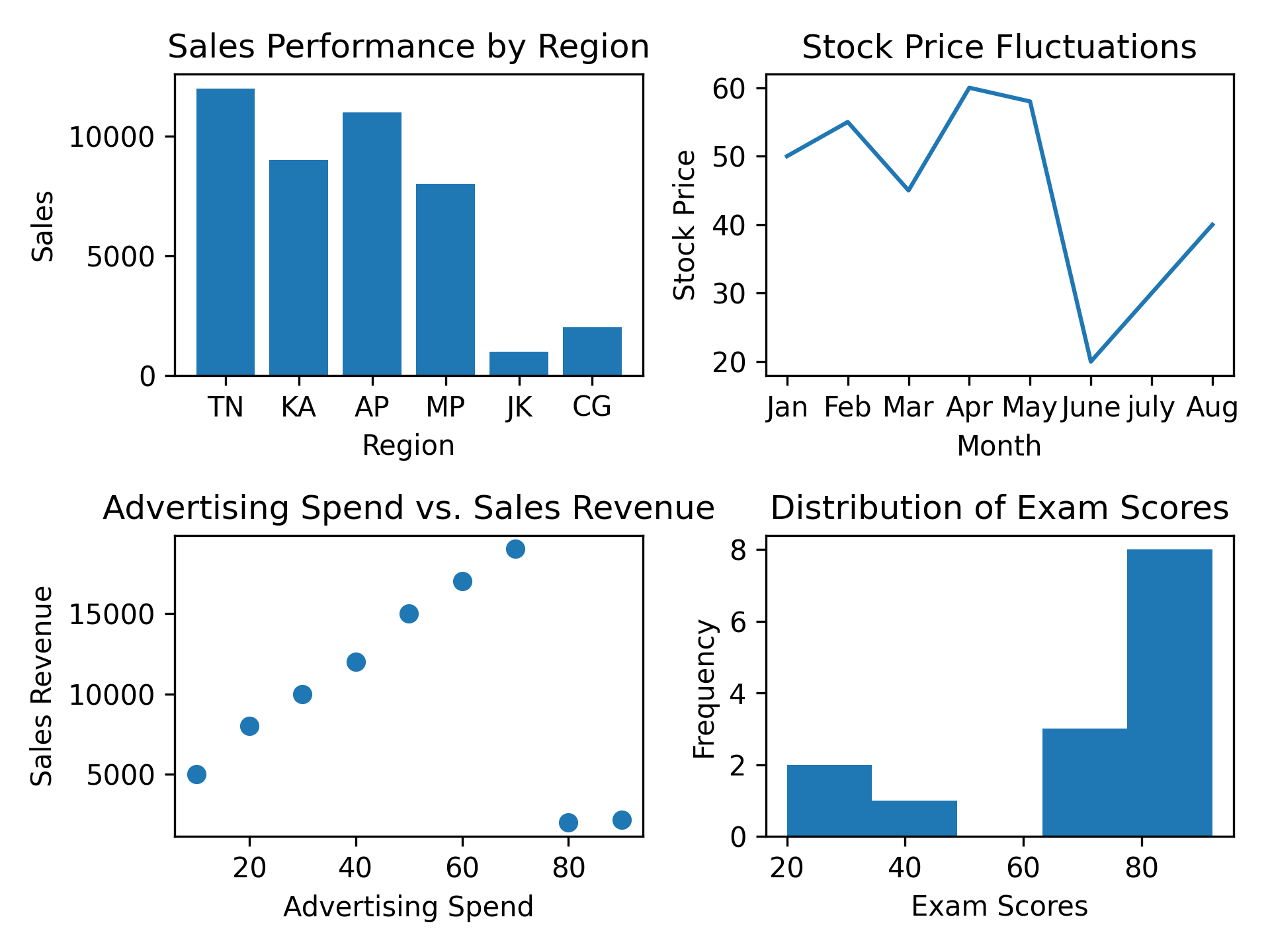
Data analysis is a crucial process that involves inspecting, cleaning, transforming, and modeling data to discover meaningful patterns, draw conclusions, ...
Read more