Table of Contents
Introduction
In the realm of statistics, the t-statistic and p-value are fundamental concepts that play a crucial role in hypothesis testing and statistical analysis. Whether you’re a student conducting research or a professional analyzing data, understanding how to find p value from t statistic is essential for making informed decisions and drawing valid conclusions. This article aims to elucidate the process of deriving the p-value from the t statistic, providing clarity on its significance and practical implications
Understanding t Statistic
The t statistic, also known as Student’s t statistic, is a measure used to assess the difference between the means of two groups or the significance of a single sample mean. It quantifies the ratio of the difference between the sample mean and the population mean to the standard error of the mean. In simpler terms, the t statistic indicates how much the sample mean deviates from the population mean in standard deviation units.
Definition and Significance
The t-statistic holds significance primarily in hypothesis testing, where it serves as the test statistic in various statistical tests, such as t-tests and analysis of variance (ANOVA). It allows researchers to determine whether the observed difference between groups is statistically significant or merely due to random variation.
The formula for Calculating t Statistic
The formula for calculating the t statistic depends on the type of statistical test being conducted. One-sample t-test formula is:

Significance of P Value
The p-value, short for “probability value,” is a measure that indicates the probability of obtaining the observed results (or more extreme results) under the assumption that the null hypothesis is true. In hypothesis testing, the null hypothesis represents the absence of an effect or relationship, while the alternative hypothesis suggests the presence of a significant effect.
Definition and Interpretation
A low p-value (< 0.05) suggests strong evidence against the null hypothesis, leading to its rejection in favor of the alternative hypothesis. Conversely, a high p-value (> 0.05) indicates weak evidence against the null hypothesis, failing to reject it. Therefore, the p-value serves as a yardstick for assessing the statistical significance of research findings.
Role in Hypothesis Testing
The p-value plays a pivotal role in hypothesis testing, guiding researchers in making decisions about the validity of their hypotheses. By comparing the p-value to a predetermined significance level (typically 0.05), researchers can determine whether the results are statistically significant and warrant further investigation.
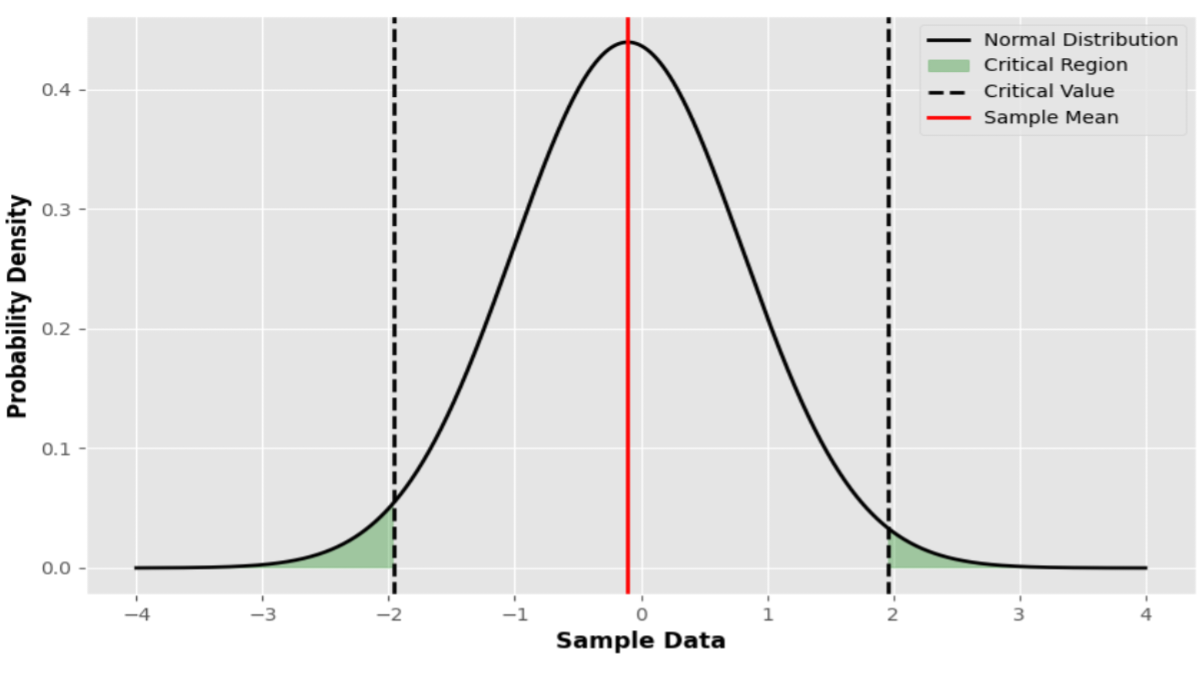
In hypothesis testing, the p-value indicates the likelihood of encountering a test statistic as unusual as, or even more unusual than, the one derived from the sample data, assuming the null hypothesis holds true. A low p-value suggests that the outcomes observed are improbable due to random chance alone, presenting evidence that contradicts the null hypothesis. Conversely, a large p-value suggests that the observed results are consistent with what would be expected under the null hypothesis, indicating that they may have occurred due to random fluctuations in the data.
When comparing the p-value to the significance level (α), researchers establish a threshold for determining the level of evidence required to reject the null hypothesis. Typically, a significance level of 0.05 is used, meaning that if the p-value is less than 0.05, the results are considered statistically significant, and the null hypothesis is rejected in favor of the alternative hypothesis. This signifies that the observed effect is likely real and not due to chance alone.
On the other hand, if the p-value is greater than 0.05, researchers fail to reject the null hypothesis, indicating that the observed results are not statistically significant. This suggests that there is insufficient evidence to conclude that the observed effect is genuine, and further investigation may be needed to draw definitive conclusions. In essence, the comparison of the p-value to the significance level provides researchers with a standardized approach to evaluating the strength of evidence against the null hypothesis. By adhering to this framework, researchers can confidently interpret the results of hypothesis tests and make informed decisions about the validity of their hypotheses, ultimately advancing scientific knowledge and understanding.
Understanding How to Find P Value from t Statistic
The t-statistic and p-value are intricately linked, with the latter being derived from the former. Understanding their relationship is crucial for interpreting the results of statistical tests accurately.
Explanation of Their Interdependence
The t-statistic and p-value both assess the likelihood of observing the sample data under the null hypothesis. As the magnitude of the t statistic increases (indicating a larger deviation of the sample mean from the population mean), the p-value decreases, signifying stronger evidence against the null hypothesis.
How P Value Is Derived from t Statistic
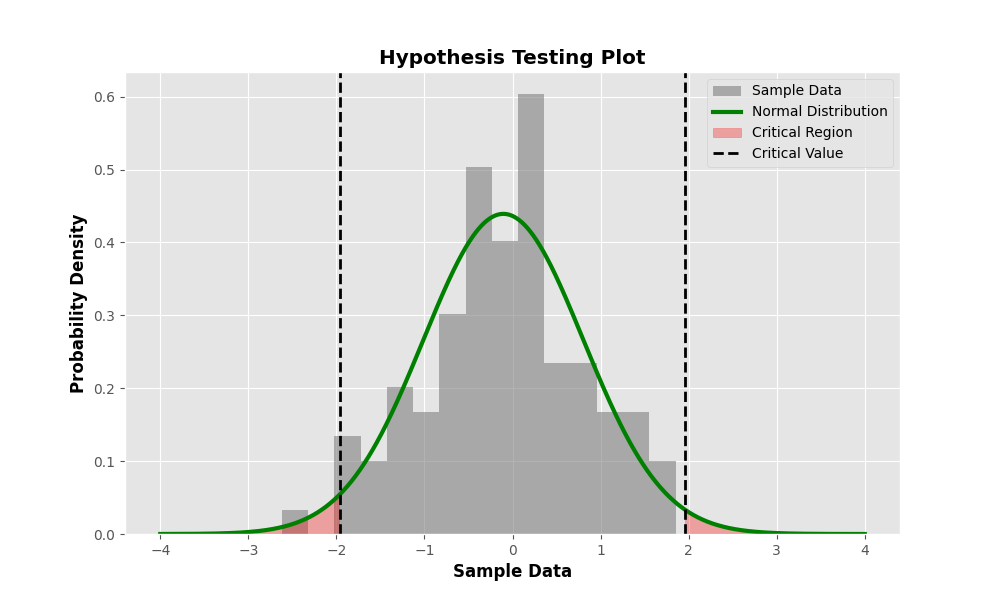
To derive the p-value from the t statistic, one typically refers to the t distribution table or uses statistical software. By comparing the calculated t statistic to the critical values in the t distribution, researchers can determine the probability of observing a t value as extreme as or more extreme than the calculated value.
Steps to Find P Value from t Statistic
While deriving the p value from the t statistic may seem daunting, following a systematic approach can simplify the process. Here’s a step-by-step guide:
Step 1: Determine the Significance Level
Before conducting the hypothesis test, specify the significance level (α), which represents the threshold for determining statistical significance. Frequently employed figures are 0.05 and 0.01.
Step 2: Find the Degrees of Freedom
The degrees of freedom (df) depend on the sample size and the type of statistical test being performed. For a one-sample t test, df = n – 1 , where n is the sample size.
Step 3: Look Up Critical Values in t Distribution Table
Consult a t distribution table or use statistical software to find the critical values corresponding to the chosen significance level and degrees of freedom.
Step 4: Calculate the P Value
Using the critical values obtained in the previous step and the directionality of the test (one-tailed or two-tailed), calculate the p-value corresponding to the observed t statistic. Statistical software or online calculators can expedite this calculation process.
Practical Examples for How to Find P Value from t Statistic
Embarking on the journey of uncovering the P value from a T statistic, let’s delve into practical scenarios where this statistical concept comes to life:
For instance:
Scenario 1: Unveiling Insights through a One-Sample T Test
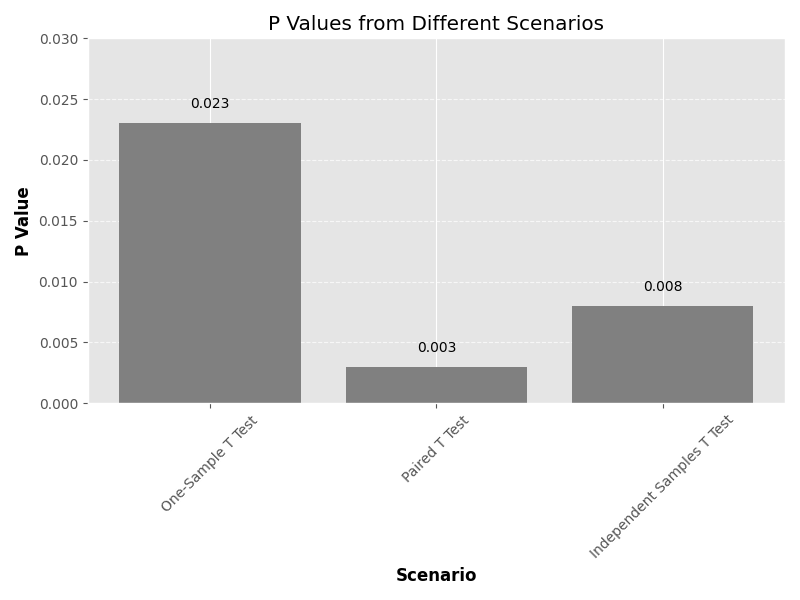
Imagine a scenario where a diligent researcher conducts a one-sample T test aiming to discern whether the average exam score of a student cohort significantly deviates from the established population mean (μ = 75). Upon meticulous calculations, the researcher derives a T statistic of 2.45, alongside degrees of freedom (df = 20). Leveraging statistical tools, they pinpoint the P value at 0.023. Given this P value’s diminutive stature compared to the significance level (α = 0.05), the researcher confidently dismisses the null hypothesis, affirming that the student cohort’s exam score markedly varies from the population mean.
Scenario 2: Unraveling Insights with a Paired T Test
Transitioning into a clinical study realm, envision researchers meticulously gauging the efficacy of a novel medication. With meticulous data collection on pre and post-medication blood pressure readings for each participant, researchers embark on a paired T test journey. Resultantly, they unearth a T statistic of -3.21, complemented by degrees of freedom (df = 29). Subsequent scrutiny reveals a P value of 0.003, indicative of statistical significance. Armed with this insight, researchers confidently affirm that the medication significantly influences blood pressure dynamics.
Scenario 3: Deciphering Distinctions via an Independent Samples T Test
Now, contemplate a study differentiating the mean cholesterol levels amid two distinct groups: patients administered a novel cholesterol-lowering drug versus those administered a placebo. Through an independent samples T test, researchers unearth a T statistic of -2.76, coupled with degrees of freedom (df = 48). Delving deeper, they discern a P value of 0.008, notably lower than the preset significance level (α = 0.05). With this revelation, researchers confidently repudiate the null hypothesis, asserting a substantial contrast in cholesterol levels between the two groups.
Importance of Correct Interpretation
While knowing how to calculate the p value from the t statistic is valuable, it’s equally essential to interpret the results accurately. Misinterpretation of statistical findings can lead to erroneous conclusions and misinformed decisions, highlighting the importance of careful analysis.
Avoiding Misinterpretation
Common pitfalls in interpreting statistical results include conflating correlation with causation, overlooking confounding variables, and misjudging the practical significance of findings. Researchers must exercise caution and critically evaluate the implications of their analyses.
Impact on Decision-Making in Research
The correct interpretation of statistical results influences subsequent research directions, policy decisions, and practical applications. By accurately assessing the significance of research findings, researchers can contribute to evidence-based decision-making and advance knowledge in their respective fields.
Common Mistakes to Avoid
To ensure the validity and reliability of statistical analyses, researchers should be mindful of common mistakes that can compromise the integrity of their findings.
Misunderstanding Significance Level
Misinterpreting the significance level (α) can lead to errors in hypothesis testing. Researchers must adhere to the chosen significance level and avoid arbitrary adjustments based on the observed p value.
Incorrect Interpretation of t Statistic
Failing to understand the implications of the t statistic can result in faulty conclusions. Researchers should interpret the magnitude and directionality of the t statistic in the context of the research question and hypotheses.
Using Improper Degrees of Freedom
Incorrectly calculating or applying degrees of freedom can distort the results of statistical tests. Researchers must accurately determine the degrees of freedom based on the study design and sample characteristics.
Tools and Resources for Calculating P Value
In the era of digital technology, researchers have access to various tools and resources that facilitate the calculation of the p value from the t statistic.
Statistical Software
Software packages such as SPSS, R, and SAS offer robust statistical capabilities, including hypothesis testing and p value calculation. These tools streamline the analysis process and provide accurate results for researchers across disciplines.
Online Calculators
Numerous websites and online platforms provide free or subscription-based calculators for conducting statistical analyses. These user-friendly tools allow researchers to input their data and obtain p values and other relevant statistics quickly.
Excel Functions
Microsoft Excel offers built-in functions for statistical analysis, including functions for calculating t statistics and p values. While not as sophisticated as dedicated statistical software, Excel can be a convenient option for basic analyses and quick calculations.
Conclusion
In conclusion, How to Find P Value from t Statistic is indispensable for conducting rigorous statistical analyses and deriving meaningful conclusions from data. By understanding the relationship between these two measures and following the prescribed steps, researchers can ensure the accuracy and validity of their findings, contributing to advancements in knowledge and evidence-based decision-making.
FAQs
Q1: What is the significance level in hypothesis testing? The significance level, often denoted as α, establishes the threshold for rejecting the null hypothesis. It signifies the maximum likelihood of committing a Type I error.
Q2: Can the p value ever be greater than 1? No, the p value always falls between 0 and 1. A value exceeding 1 would lack coherence within the context of probability.
Q3: How can I determine the p value from a t statistic, and what is the role of degrees of freedom in this calculation? A: The understanding of degrees of freedom holds pivotal importance when calculating the p value from a t statistic. Essentially, degrees of freedom signify the independent information pieces within the sample data. For t tests, degrees of freedom are derived by subtracting one from the total observations. They shape the t statistic’s distribution and dictate the critical values, significantly impacting the p value determination. By comprehending degrees of freedom, researchers can effectively interpret hypothesis test outcomes and make well-informed decisions based on statistical significance.
Q4: Why is it crucial to utilize the accurate degrees of freedom in computations? Degrees of freedom directly influence the t distribution’s shape and the critical values used in hypothesis testing, underscoring the necessity for precise calculations to ensure valid results.
Q5: How do I calculate the p value from a test statistic, and what role does the significance level (α) play in hypothesis testing? A: In determining the p-value from a test statistic, the significance level (α) serves as a pivotal threshold for establishing statistical significance. Researchers typically predefine the significance level before conducting the hypothesis test, commonly opting for values like 0.05 or 0.01. This level represents the utmost probability of committing a Type I error, wherein the null hypothesis is erroneously rejected. By comparing the calculated p-value with the significance level, researchers ascertain the statistical significance of observed results and decide whether rejecting the null hypothesis is warranted.
Read more